Rechner ↑Inhalt ↑
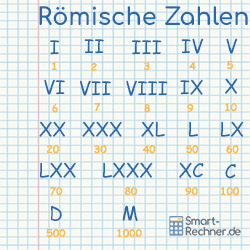Römische Zahlen - oft auch lateinische Zahlen genannt - sind in der römischen Antike entstanden. Die aus einzelnen Zahlzeichen
zusammmengesetzte Schrift wird heute noch für Nummern, ein bestimmtes Datum, auf Ziffernblättern und für andere besondere Zwecke genutzt.
In der heute gebräuchlichen Form sind die lateinischen Buchstaben I (1), V (5), X (10), L (50), C (100), D (500) und M (1000) als Zahlzeichen
enthalten.
Anders als im üblichen Dezimalsystem, basiert der Wert römischer Zahlen auf der Addition der einzelnen Zahlzeichen bzw. Symbole. Daher
wird es auch additives Zahlsystem genannt. Der Wert der einzelnen arabischen Ziffern einer Zahl im Dezimalsystem ist hingegen von der jeweiligen
Stelle der Ziffer abhängig, so dass von rechts nach links Einer, Zehner, Hunderter usw. summiert werden. Es wird daher Stellenwertsystem genannt.
Bereits in der Grundschule lernen Schüler die römischen Zahlen kennen. In den weiterführenden Schulen werden die römischen Zahlen dann
im Mathematikunterricht vertieft.
Ein Datum in römischen Zahlen darstellen
Wenn Sie ein beliebiges Datum in eine römische Zahl umwandeln möchten, empfehlen wir Ihnen unseren Themenbereich
Römisches Datum.
Dort können Sie die Umrechnung mit Hilfe unseres weiteren Smart-Rechners bequem durchführen.
Rechner ↑Inhalt ↑
Herr Marmor ist Steinmetz und möchte das Jahr 2024 in römischen Zahlen meißeln. Zur Umrechnug der Dezimalzahl 2024 in die
gewünschte römische Zahl geht er schrittweise folgendermaßen vor:
Als erstes wird die höchste Stelle von 2024, also die zwei Tausender in eine römische Zahl umgerechnet. Angewendet wird hierzu
die oben beschriebene Additionsregel "Ein kleineres Symbol nach einem größeren Symbol wird addiert. Ebenso alle führenden M."
Die zweite umzuwandelnde Ziffer von 2024 ist die Null. Römische Zahlen haben und brauchen allerdings für Null kein gesondertes Symbol,
weshalb sie zu einem "leeren Zeichen" umgewandelt wird.
Die dritte umzuwandelnde Ziffer von 2024 ist die 2. Diese wird wieder gemäß der Additionsregel berechnet.
Die vierte umzuwandelnde Ziffer von 2024 ist die 4. Die 4 könnte man als römische Zahl mittels IIII darstellen. Da aber gemäß der heutigen Regeln
vier gleiche Zeichen hintereinander vermieden werden sollen, wird die 4 nun anhand der oben beschriebenen Subtraktionsregel dargestellt:
"Ein kleineres Symbol vor einem größeren Symbol wird subtrahiert." Statt IIII schreiben wir IV, also 5 minus 1.
Die Einzelergebnisse der vier vorherigen Schritte müssen schließlich nur noch aneinandergereiht werden, um die gewünschte römische Zahl zu erhalten:
MM, XX und IV ergibt schließlich MMXXIV
Rechner ↑Inhalt ↑
In Petras Schulunterricht werden gerade die römischen Zahlen behandelt. Petra soll nun die römsche Zahl MCCXXXIV in eine Dezimalzahl umrechnen.
Sie geht wie folgt vor: Petra geht die römische Zahl von links nach rechts durch, um jedes Symbol in seine Dezimalzahl umzurechnen.
Da in MCCXXXIV gleich zwei C hintereinander auftreten, kann man den Wert beider C hintereinander umrechnen:
Da in MCCXXXIV gleich drei X hintereinander auftreten, kann man den Wert aller drei X hintereinander umrechnen:
Für das abschließende IV in MCCXXXIV kommt die Subtraktionsregel ins Spiel, denn hier steht mit dem I ein kleineres Symbol vor
dem größeren V. Somit wird das I vom V abgezogen:
Die Einzelergebnisse der vier vorherigen Schritte müssen schließlich nur noch addiert werden, um die gewünschte Dezimalzahl zu erhalten,
also 1000 + 200 + 30 + 4 = 1234
Rechner ↑Inhalt ↑
Im Folgenden präsentieren wir Ihnen einige Fragen zu den römischen Zahlen nebst den dazugehörigen Antworten.
Nein, die alten Römer kannten noch keine Null für ihr Zahlsystem. Eine additive Zahlschrift, wie es die römische ist, benötigt keine Null.
Für die Null gibt es daher kein Zeichen in römischen Zahlen. Nicht zuletzt wegen der fehlenden Null ist das Ausführen komplizierter Berechnungen
mit römischen Zahlen nur bedingt möglich.
Gemäß der im Schulunterricht vermittelten Regeln dürfen nur drei römische Ziffern hintereinander stehen, also z.B. III, XXX oder CCC.
Denn die sogenannte Subtraktionsregel sorgt dafür, dass man mit drei hintereinder stehenden Zeichen auskommt, um eine beliebige Zahl
darzustellen. Die Subtraktionsregel besagt, dass ein kleineres Symbol vor einem größeren Symbol subtrahiert wird. Somit kann man
beispielsweise zur Darstellung der Zahl 4 die vier Zeichen IIII vermeiden, indem man stattdessen IV, also 5 minus 1 schreibt.
Die römischen Zeichen der Fünferbündelung, also V, L und D für 5, 50 und 500 dürfen hingegen nur einmal hintereinander genutzt werden,
da etwa VV durch X bzw. LL durch C zu ersetzen ist.
Die Tatsache, dass nur drei Zeichen hintereinander stehen dürfen, führt jedoch dazu, dass der größte Wert einer römischen Zahl
3.999 = MMMCMXCIX beträgt. Denn ab 4.000 müssten vier M hintereinander genutzt werden. Dies wurde entweder durch die Defintion weiterer
Zeichen für 5.000 (ↁ), 10.000 (ↂ) usw. vermieden oder auch durch einen Multiplikator für die Anzahl der Ms, also etwa X•M für 10×M=10.000.
Römische Zahlen wurden und werden zur Darstellung von Zahlen genutzt. Sie eignen sich allerdings nur bedingt zum Rechnen.
Während das schriftliche Multiplizieren, Dividieren oder auch Subtrahieren römischer Zahlen wegen der dort fehlenden Null kaum möglich ist,
kann immerhin eine Addition zweier römischer Zahlen vorgenommen werden, indem man die einzelnen Zeichen schrittweise addiert. Z.B. ist
26 + 15 = XXVI + XV = XXXVVI = XXXXI = XLI = 41.
Dies funktioniert aber wieder nur bedingt, sobald in den zu addierenden Zahlen z.B. eine 4 vorkommt, für deren Umwandlung in eine römische
Ziffer das Subtraktionsverfahren ("Ein kleineres Symbol vor einem größeren Symbol wird subtrahiert") angewandt wird. Dann wird es mit der
Addition von z.B. 26 + 14 schon schwierig: 26 + 14 = XXVI + XIV = XXXVIIV = ?
Wie oben bereits beschrieben, gibt es sieben römische Zahlzeichen: I (1), V (5), X (10), L (50), C (100), D (500) und M (1000).
Vereinzelt gibt es für größere römische Zahlen weitere Zeichen, wie etwa ↁ für 5.000, ↂ für 10.000 u.a.
Die sieben Zeichen werden häufig in Zeichen mit Zehnerbündelung (I, X, C und M) und Zeichen mit Fünferbündelung (V, L und D) unterteilt.
Die vier Zeichen mit Zehnerbündelung bilden die Grundziffern und die drei Zeichen mit Fünferbündelung sind die Zwischenziffern.
Geben Sie bitte wahlweise eine Dezimalzahl oder eine römische Zahl, also eine Zeichenkette bestehend aus den Groß- oder
Kleinbuchstaben M, D, C, L, X, V oder I ein. Der Rechner erkennt automatisch, welches Zahlenformat Sie eingegeben haben
und rechnet entsprechend eine Dezimalzahl in eine römische Zahl um bzw. wandelt umgekehrt eine römische Zahl in eine Dezimalzahl.